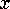 and
and 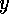 ) coordinate system,
) coordinate system, 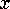 will denote
horizontal position, and
will denote
horizontal position, and 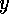 will denote vertical position.
will denote vertical position.
 Hints
Hints
 Session 8: Week 16/17: Projectiles
Session 8: Week 16/17: Projectiles
 Session 8: Week 16/17: Projectiles
Session 8: Week 16/17: Projectiles
The purpose of this exercise is to calculate the theoretical trajectory of a projectile in a constant gravitational field. In other words, we want to calculate the path followed by, say, a ball thrown in the air.
We are going to make some simplifications. We will work in just two dimensions (i.e. as if we are looking exactly side on at the path of the ball). We will also neglect air resistance, and will treat the projectile as a point mass. This allows a simple analysis of the motion of the projectile, using newtonian theory.
In our two dimensional (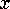 and
and 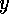 ) coordinate system,
) coordinate system, 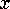 will denote
horizontal position, and
will denote
horizontal position, and 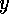 will denote vertical position.
will denote vertical position.
The initial value of 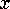 will be taken as zero.
will be taken as zero.
A zero 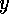 value will correspond to the projectile being on the ground.
The initial value of
value will correspond to the projectile being on the ground.
The initial value of 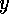 will be some positive value (in effect, the
height of the person throwing the ball).
will be some positive value (in effect, the
height of the person throwing the ball).
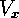 will denote the horizontal component of velocity, and
will denote the horizontal component of velocity, and 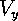 the
vertical component. We will assume that both
the
vertical component. We will assume that both 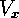 and
and 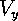 are
initially positive. Similarly,
are
initially positive. Similarly, 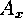 and
and 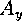 will be the components of
acceleration.
will be the components of
acceleration.
The "initial" information provided for a particular run of the program
will be the initial
height (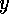 ) and initial velocity components (
) and initial velocity components (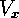 and
and 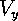 ) of the
projectile. These values will be assigned to suitable variables. You can
either code values directly into the program (in which case you will
have to change the program, and recompile, every time you want to try
different values) or you can have the program prompt for and read in
values when it starts running.
) of the
projectile. These values will be assigned to suitable variables. You can
either code values directly into the program (in which case you will
have to change the program, and recompile, every time you want to try
different values) or you can have the program prompt for and read in
values when it starts running.
The output from the program will be a print out on the screen of
the numerical values
of 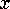 and
and 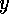 at successive, "small", intervals of time. The program
should terminate when
at successive, "small", intervals of time. The program
should terminate when 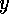 becomes zero again (i.e. the projectile falls
back to earth). This print out may be captured into a text file
and a graph plotted of
becomes zero again (i.e. the projectile falls
back to earth). This print out may be captured into a text file
and a graph plotted of 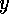 versus
versus 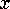 (one way of doing this
is described in detail in
the Hints section below).
(one way of doing this
is described in detail in
the Hints section below).
Informally, the motion of the projectile is pretty simple: it moves
steadily to the right (positive 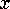 direction), simultaneously going up
for a while (positive
direction), simultaneously going up
for a while (positive 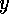 direction), and then coming down again to
land.
direction), and then coming down again to
land.
Formally, at each time step, the new 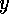 co-ordinate can be calculated
as:
co-ordinate can be calculated
as:
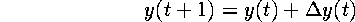
where (approximately):

In words, if the velocity in the 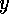 direction is
direction is 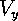 , then, in a time
, then, in a time
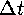 , the projectile will move a distance of
, the projectile will move a distance of 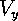 multiplied by
multiplied by
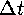 ; and the new
; and the new 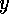 position is the old
position is the old 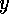 position plus this
movement. This calculation would be exact if
position plus this
movement. This calculation would be exact if 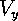 were constant; if
were constant; if 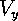 is changing (as it will be in our case) then
the calculation will still be approximately correct, as long as
is changing (as it will be in our case) then
the calculation will still be approximately correct, as long as
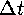 is "small" - namely small enough that the percentage change
in
is "small" - namely small enough that the percentage change
in 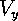 in that time is "negligible". Of course, you can only
estimate this once you have some idea of how quickly
in that time is "negligible". Of course, you can only
estimate this once you have some idea of how quickly 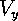 will be
changing...
will be
changing...
The new 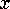 co-ordinate may be calculated similarly.
co-ordinate may be calculated similarly.
Now, in principle, both 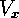 and
and 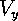 could also be
simultaneously changing, and have to be recalculated, at each time step.
But since we are neglecting air resistance, and since gravity works
straight down, there will be zero acceleration in the
could also be
simultaneously changing, and have to be recalculated, at each time step.
But since we are neglecting air resistance, and since gravity works
straight down, there will be zero acceleration in the 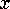 direction
(
direction
(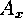 is zero), so that
is zero), so that 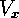 will actually remain constant, equal to
its initial value. There will be acceleration in the
will actually remain constant, equal to
its initial value. There will be acceleration in the 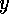 direction
however, of value
direction
however, of value 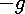 , where
, where 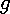 is the acceleration due to gravity at
the surface of the earth (about 9.81 meters per second per second).
This is negative because our
is the acceleration due to gravity at
the surface of the earth (about 9.81 meters per second per second).
This is negative because our 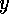 co-ordinate is positive in the upward
direction and gravity works downward (last time I checked anyway...).
This acceleration in the
co-ordinate is positive in the upward
direction and gravity works downward (last time I checked anyway...).
This acceleration in the 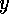 direction will be constant (since
direction will be constant (since 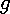 is
not changing). Thus, the new
is
not changing). Thus, the new 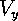 at each time step can be calculated
as follows:
at each time step can be calculated
as follows:
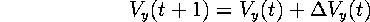
where:

That is, the change in the (vertical) component of speed is simply the
(vertical) acceleration multiplied by the time it acts over; and the new
speed is simply the old speed plus this change.
You should test your program carefully. Explain, in your report, what tests you carry out, how the program behaves, and whether it has passed such tests.
 Hints
Hints
 Session 8: Week 16/17: Projectiles
Session 8: Week 16/17: Projectiles
 Session 8: Week 16/17: Projectiles
Session 8: Week 16/17: Projectiles