Some Remarks on Autocatalysis and Autopoiesis
Barry McMullin
http://www.eeng.dcu.ie/~mcmullin/
©1999
Presented at the workshop
Closure: Emergent Organizations and their Dynamics
May 3-5, 1999, University of Ghent, Belgium.
Abstract:
The notions of collective autocatalysis and of
autopoiesis are clearly related; equally clearly, they are not
quite the same. The purpose of this paper is to try to clarify
the relationship. Specifically I suggest that autopoiesis can
be at least roughly characterized as ``collective autocatalysis
plus spatial individuation''. While some
mechanism of spatial confinement or concentration is probably
necessary to the effective operation of
any collectively
autocatalytic reaction network, autopoiesis requires, in
addition, that the mechanism for maintaining this confinement
should itself be a product of the reaction network--and should
thus (?) be capable of separating or individuating otherwise
identically organized networks.
I suggest an informal heuristic test to discriminate the
(merely) collectively autocatalytic from the (properly?)
autopoietic. Finally, in the light of this, I review a variety
of published abstract or model systems
(Alchemy, 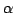 -universes, Tierra, SCL).
-universes, Tierra, SCL).
Keys: Autopoiesis, Collective Autocatalysis, Individuality,
Artificial Life.
The concept of autopoiesis was originally formulated by
the Chilean biologists Francisco Varela and Humberto Maturana as
being ``necessary and sufficient to characterize the organization
of living systems'' (Maturana & Varela, 1973, p. 82). They
conceived of autopoiesis as specifying an organization which
might be realizable with a variety of material components--not
just the specific biochemical molecular species that happen to be
characteristic of life on Earth. Indeed, to illustrate this,
they described a model system, implemented as a computer program,
where autopoietic organization could be realized with just three
distinct kinds of component
(Varela et al., 1974).1
The notion of autopoiesis has been extended and applied in a wide
variety of domains, including linguistics, social organization,
and family therapy. However, my own interest in the theory is
strictly concerned with its original ``molecular'' formulation,
as a description of the characteristic autonomy of even the
simplest living organisms, conceived as a special category of
essentially chemical system. The discussion here will be
strictly limited to this ``molecular'' or ``chemical''
autopoiesis.
To the extent that autopoiesis correctly captures something like
a minimum condition for living phenomenology, it has an obvious
connection to discussions of the origin of life. Indeed,
in the autopoietic framework, the origin of life is essentially
identical with the origin of molecular autopoiesis
(Maturana & Varela, 1973, pp. 93-95).
Much more recently, the concept of a ``collectively
autocatalysis'' has been presented by Stuart Kauffman as being
critically involved in, if not identical with, the origin of life
(Kauffman, 1993). However, Kauffman makes no explicit
reference to autopoiesis.
My purpose here then is primarily to attempt such an explicit
comparison between the notions of autopoiesis and collective
autocatalysis.
An autopoietic machine is a machine organized (defined as a
unity) as a network of processes of production (transformation
and destruction) of components that produces the components
which:
- (i) through their interactions and transformations
continuously regenerate and realize the network of processes
(relations) that produced them; and
- (ii) constitute it (the machine) as a concrete entity in the
the space in which they (the components) exist by specifying
the topological domain of its realization as such a network.
Maturana & Varela
(1973, pp. 78-79)
This is the canonical definition of autopoiesis offered by
Maturana and Varela. In the specific case of molecular
autopoiesis, it seems clear that the ``components'' should be
interpreted as individual molecules, and the ``processes of
production'' are essentially chemical reactions. It is not quite
so clear what it means for these molecules to ``continuously
regenerate and realize the network of processes that produced
them''. Elsewhere, the following qualification is offered:
Consider for example the case of a cell: it is a network of
chemical reactions which produce molecules such that
- (i) through their interactions generate and participate
recursively in the same network of reactions which produced
them, and
- (ii) realize the cell as a material unity.
Varela et al. (1974, p. 188)
Still, it is not clear what is the force of the phrase ``generate
and participate recursively''. Specifically, is ``generating'' a
chemical reaction a distinct thing from ``participating'' in one?
Having reference to the (highly schematic) computer
model presented by Varela et al. (1974), it seems plausible
to interpret ``participating'' in a reaction as meaning simply to
be a reactant; whereas ``generating'' a reaction might mean to
catalyse it. Catalysts are also, of course ``reactants'';
but their special property is that they emerge unchanged from the
catalysed reaction, while drastically increasing the reaction rate.
In the limiting case, the un-catalysed reaction may occur with
negligible rate, whereas, in the presence of catalyst, it may
occur at a rate which has significant manifestations in the
system. In such a case, it seems reasonable to say that the
catalyst ``generates'' the reaction (given the availability of
the other reactants).
So the first condition for molecular autopoiesis is that the
reaction network which characterizes the organization of the
system must produce all the species of molecular component which
are considered to materially constitute the system, and
these components must themselves generate the reaction
network, in the sense of catalysing some (or all?) of the
reactions (which would otherwise occur at negligible rate).
There are still some significant ambiguities here. How, for
example, do we determine which components materially
``constitute'' the system? In the computer model of molecular
autopoiesis there is one component, performing a specifically
catalytic function, which is not itself produced by any
reaction in the network--so should it not be regarded as a
material component of the system? There are also ``substrate''
particles which are not--or at least, not
necessarily--produced through the constituent reactions
of the system (i.e., they may be produced by the reaction
network, but may alternatively ``drift'' in from the external
ambience). Also in this model there are two reactions
(``concatenation'' and ``disintegration'') which are not
catalysed at all--and thus arguably not ``generated'' by the
system.
I should note that Varela et al. (1974) do present a
6-point ``key'' for determining whether or not a specific system
should be regarded as autopoietic. This seems to suggest, for
example, that it is acceptable for some of the components not to be
produced by reactions in the system, provided that they
``participate as necessary permanent constitutive components in
the production of other components''. This may account for the
case of the catalytic component in the model system--though I
would suggest that the meaning is still less than precise.
In any case, let us now move on to the second defining condition
for autopoiesis. This is that the system itself must specify
``the topological domain of its realization''. The essential
idea here seems to be that the same network of chemical processes
which is used to identify the system as such, must also have the
effect of locating or demarcating the system in space. The
system must, in other words, establish some sort of boundary
between ``itself'' and the rest of the universe in which it is
embedded.
In the specific case of biological cells, this boundary is
manifested in the external membrane of the cell. In the
simplified computer model (which exists in a two dimensional
universe), this boundary consists of a closed linear chain of
molecules. It seems that, in the case of molecular
autopoiesis, the boundary performs at least the function of
limiting or controlling the spatial diffusion of the molecules
constituting the system. This is presumably necessary because,
in the absence of such control on diffusion, the reactant
concentrations may dilute to the point where one or more of the
defining reactions effectively ceases to operate, and the whole
self-sustaining reaction network then breaks down.
The basic notion of an ``autocatalyst'' is a molecular
species which, in the presence of suitable reaction substrates,
catalyses a reaction in which one or more molecules of that same
catalyst molecular species are among the reaction products--over and
above the original catalyst molecule itself. Note carefully the
distinction here between the original catalyst molecule
which--by definition--emerges unchanged from the catalysed
reaction; and the one or more additional catalyst
molecules which are among the reaction products.
If we assume that the uncatalysed reaction occurs at negligible
rate then, in the absence of any catalyst molecules, the
substrates will remain unreactive; but if the medium is seeded or
innoculated with one or more catalyst molecules this would then
trigger production of more catalyst so that the reaction would
actually proceed at an accelerating rate until limited by
the availability of the substrate. If the reaction takes place
in a flow reactor, where substrate is continuously provided, and
the reaction product removed, then the reaction could evidently
sustain itself indefinitely.
Autocatalytic molecules may also be termed ``self-replicating''
in a reasonable sense. This has an obvious biological relevance
in the exploitation of such molecules as genetic information
carriers. This usage depends on the existence of a large set of
distinct molecules (which can thus carry ``information'' via
their distinctions) but which are all individually autocatalytic,
thus allowing for the generation of informational ``copies'' for
distribution to offspring.
The autocatalytic molecules which play this role, in modern
organisms at least, are the nucleic acids. Note, however,
that nucleic acids are themselves rather complex; and require
complex substrates (nucleotides) and additional catalysts
(replicases) in order to manifest their autocatalytic activity.
So while autocatalytic molecules, per se, can be very useful and
play a key role in modern organisms, it is doubtful whether such
molecules could participate in the spontaneous emergence or
origin of life.
In response to this, Stuart Kauffman has proposed that, while
individually autocatalytic molecules might be rather unlikely to
arise (or even sustain themselves) spontaneously, the same is
not necessarily true for sets of molecular species
which mutually catalyse each others production. The idea here is
to consider sets of molecular species such that none of them need
be individually autocatalytic (which may be an unfeasible
requirement), but where production of every element of the set is
effectively catalysed by at least one other member of the same
set. In such a situation the whole set is said to be
collectively autocatalytic.
In just the same way as sketched out for an individually
autocatalytic molecular species, we can imagine seeding a flow
reactor with a collectively autocatalytic set of species (at
least one molecule from each member of the set). Again, provided
we maintain a flow of some basic substrate molecules (the
``exogenous food set'' in Kauffman's terms) there should now be
the possibility of an indefinitely sustained, self-reinforcing,
reaction network, continuously producing more molecules of all
the species in the set.
It is clear that the notion of an autocatalytic set is closely
related to the first element of the definition of
autopoiesis. Both involve the idea of a ``closed'' reaction
network which may therefore be able to dynamically sustain itself
indefinitely--subject to the availability of some basic
``substrate'' materials and the overall reaction kinetics etc.
The definition of autopoiesis is, admittedly, somewhat ambiguous
about the role of catalytic activity as such; but the
computer model certainly explicitly involves at least one
catalysed reaction, without which the putative reaction
network could not be closed. Conversely, while the
reaction networks posited for collective autocatalysis seem to be
technically limited to include only catalysed reactions,
there doesn't seem to be any particular difficulty about allowing
some uncatalysed reactions to participate also; if anything, this
possibility should slightly improve the prospects for the
spontaneous emergence of such sets.
In trying to isolate more precisely what it is that both the
notions of autopoiesis and collectively autocatalytic sets seem
to share, I suggest it may be useful to think about the following
more concrete scenario. Suppose we have a flow reactor, with a
flow of some specified ``substrate'' or ``food set'' materials
through it. There may be some reactions which occur
spontaneously, at significant rates, among these, but we
essentially discount such reactions (or assume they run to
equilibrium etc.). Now suppose it is the case that this reactor
can be seeded with some set of further molecular species, such
that a reaction network is then established which sustains
the presence of these same molecular species under flow
conditions. This new network may involve some
uncatalysed reactions (which did not previously occur because
the relevant reactants did not arise); but it must necessarily
involve at least one reaction which must be catalysed, and such
that the catalyst species itself gets produced (directly or
indirectly) only if this catalysed reaction takes place.
Let me call any reaction network with this property ``collectively
self-sustaining''.
I suggest that this notion is at once both somewhat stronger and
somewhat weaker that Kauffman's ``collectively autocatalytic
set''. It is weaker because it allows the inclusion of
some uncatalysed reactions. If anything, this relaxation
should make it easier for such networks to arise, and would thus
strengthen Kauffman's claims for the spontaneous emergence of
such networks. However, it is stronger than Kauffman's notion in
that it explicitly asks for the reaction network to be
self-sustaining in practice--under some specific reaction
conditions, and associated reaction kinetics; the collectively
autocatalytic property, on the other hand, is a purely
topological characteristic of a reaction network
graph--indicating only the possibility of a
self-sustaining network under some otherwise unspecified
conditions. Of course, as a practical matter in the origin of
life, only reaction networks which are actually
self-sustaining under some reasonably feasible conditions can
play any significant role.
The relationship between the idea of a self-sustaining network
and autopoiesis is somewhat more obscure. Certainly, autopoiesis
shares the requirement for actual (as opposed to ``potential'')
self-maintenance, and would seem to have a similar requirement
for some sort of (catalytic?) ``closure''. Yet, it also seems
that autopoiesis does not promise a reaction network that would
sustain itself under ``open'' flow conditions. In particular, as
already mentioned, in the simplified computer model the molecular
species termed ``catalyst'' does not get produced by any reaction
in the network. Under flow conditions either catalyst would flow
out without replacement and the reaction network would break
down, or catalyst would have to be continuously supplied as a
component of the ``food set''; but in the latter case the
``autopoietic'' reaction network would be immediately and
unconditionally instantiated, rather than being contingent on
seeding. On the face of it this suggests that autopoiesis is a
significantly weaker notion than that of self-sustaining network,
even to the point of being too weak to be of any interest.
But of course, autopoiesis was not intended to deal with an
``open'' flow reaction condition; instead it is concerned with
very special flow conditions. Special firstly in that they can be
(or must be?) selective--in the sense of something like a
semi-permeable membrane; but special secondly in the requirement
that the constraints on flow should themselves be a result or
consequence of the autopoietic reaction network. It is this
requirement for the reaction network to exhibit these two
different kinds of closure--closure of the reaction network
together with spatial closure--that critically demarcates
autopoiesis per se, and makes it a significantly stronger and
more interesting idea than a self-sustaining reaction network alone.
Maturana and Varela themselves have been clear from their
earliest descriptions of autopoiesis that this spatial or
topological separation is a critical distinction between their
concept and autocatalysis per se:
Autocatalytic processes do not constitute autopoietic systems
because among other things, they do not determine their
topology. Their topology is determined by a container that is
part of the specification of the system, but which is independent
of the operation of the autocatalysis. Processes of this
or similar kind are abundant in the physical space.
Maturana & Varela
(1973, p. 94, emphasis added)
I suggest that we might interpret Kauffman's work on the
emergence of collective autocatalysis as, in significant part, a
more formal and rigorous demonstration of the rather bold
assertion at the end of this quotation. It should be noted that
Kauffman is certainly well aware that spatial enclosure is a
significant issue in this area. For example, he stipulates
explicitly that, for the reactions of a putatively autocatalytic
set to occur ``effectively'' then the reactants ``must be
confined to a sufficiently small volume''
(Kauffman, 1993, p. 298). However, while he goes on to
consider some candidate mechanisms for providing such confinement
(e.g., coascervates, proteinoid microspheres, liposomes) it is
not clear to me whether he attaches any particular importance to
the idea that these containment devices should themselves be
produced and maintained as products of the contained reaction
network--which seems to be the decisive extra constraint
involved in autopoiesis.
I have suggested that (molecular) autopoiesis and collective
autocatalysis are closely related ideas. Both involve something like
a self-sustaining reaction network, and both require some
mechanism of spatial localization or confinement for effective
operation. The critical distinction is that autopoiesis
specifically requires that this confinement should itself be in
some sense a product of the confined reaction network, whereas
collective autocatalysis is assumed to rely on some independent
confinement mechanism.
This seems to me clear enough as far as it goes; but I still have
some difficulty in deciding whether the full requirement of
autopoiesis is met in particular cases. Specifically, consider
the computer model system offered by Varela et al. (1974).
It is true that, in this case, there is a cleavage of the space
which confines the reaction network, and which is maintained as a
specific consequence of the reaction network. However, it is
also true that, as an integral aspect of the ongoing behaviour of
this autopoietic system, the spatial boundary or membrane is
regularly ruptured. The membrane is subsequently repaired
again--and, indeed, this is arguably the chief phenomenon of
interest in this system. Nonetheless, the fact that the spatial
localization is regularly interrupted in this way makes it more
difficult to be clear what exactly the ``topological''
autopoietic requirement or criterion is.
So I would like to suggest the following informal and heuristic
test. Consider two instances of the same collectively
self sustaining reaction network. For the moment I suppose that
we do not know whether these should qualify as autopoietic or
(merely) collectively autocatalytic. They are considered as
instances of the same reaction network in the sense that the same
set of molecular species is present in both cases; but they are
separate instances in the sense that each is constituted
(instantaneously) by distinct collections of individual
molecules. Specifically I assume that, initially, they have been
prepared or instantiated in separate reaction ``vessels'' (in the
manner of the independent confinement mechanism already posited
to support the continued operation of a collectively
autocatalytic set). Now consider the situation if the contents
of both vessels are ``mixed'' together. I assume that there will
be continued availability of any necessary food set materials
etc., so that the self-sustaining behaviour of the network(s) can
continue unchanged. The key question now is whether there will
still meaningfully be two instances of the reaction network or
just one. That is, in the absence of any imposed spatial separation
mechanism, do the networks themselves maintain their
individuality? I would suggest that, if they do, then this
reaction network may reasonably be classified as meeting the
autopoietic criterion ``for specifying the topological domain of
its realization''; whereas if not, then the network should be
regarded only as collectively autocatalytic.
The Alchemy system was formulated by Walter Fontana and
Leo Buss in an explicit attempt to examine the abstract
problem of the emergence of biological organization
(Fontana & Buss, 1994b,a).
An Alchemy universe or reactor embodies the abstract
notion of molecular species, with internal, compositional,
structure, and characteristic reactions between instances of
these species. All reactions may be characterized as
``catalytic'' in the sense that the original reactants are
preserved, unchanged. (This is possible because, in this abstract
system, there is no ``conservation of matter'' so that reaction
products can be created without any consumption of reactants.)
There is no notion of ``space''--any reactant can potentially
react with any other (this is also referred to as a
``well-stirred'' reactor).
Reactions are deliberately specified to occur under flow
conditions--so that particular sets of molecular species can
continue to inhabit the reactor on an ongoing basis only if they
(collectively) regenerate themselves. Thus, by definition,
only collectively autocatalytic sets can persist for
extended periods in the Alchemy system.
Several different experimental arrangements and outcomes have
been described. Briefly, if the possibility of
individually autocatalytic molecules is allowed (the
``Level 0'' experiments) then reactors quickly become dominated
either by one such species, or a co-operative network of such
species. The latter connects these results with the
Hypercycles of Eigen & Schuster (1979). Such
networks are found to be unstable under perturbation and collapse to
single autocatalytic species. If individual autocatalysis is
dis-allowed (the ``Level 1'' experiments), then the
spontaneous emergence and persistence of collectively
autocatalytic reactions networks is reliably observed. This is
consistent with Kauffman's analyses. Unlike the previous case,
these networks tend to be rather stable under perturbation.
A further set of experiments (``Level 2'') considers the results
of ``mixing together'', in one reactor, collectively autocatalytic
sets that have first emerged in independent reactors. This is
clearly related to my heuristic test for autopoiesis; but it
differs critically in that the networks being brought together
are different, rather than distinct instances of the same
network. The results of these experiments are interesting in
their own right, but do not relate to my concerns here. On the
contrary, it seems clear that, because Alchemy
deliberately eschews any notion of spatial structure in a reactor,
there is no mechanism for spatial separation or containment.
Therefore, even in the absence of any specific experiment, it
seems that, if two instances of the same network are placed in a
single reactor then they instantly lose all individuality, and
become just a single instance.
Thus, although Fontana and Buss refer to Alchemy as
being related to work on autopoiesis (as, indeed, it certainly
is), I think that the collectively autocatalytic reaction
networks exhibited should certainly not be considered as
autopoietic; and given the deliberate elimination of spatial
notions from the model, it seems that autopoietic organization
cannot emerge, or be embedded, in such systems.
The 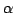 -universes are a category of abstract or model
systems devised by John Holland over 20 years ago
(Holland, 1976). They were loosely
inspired by notions of basic biochemical organization, and were
devised specifically to consider some issues in the spontaneous
emergence of life. The systems are, broadly speaking,
``artificial chemistries'', with notions of atoms, molecules, and
reactions between them (both catalysed and uncatalysed). There
is an explicit notion of space, albeit only
one-dimensional.
-universes are a category of abstract or model
systems devised by John Holland over 20 years ago
(Holland, 1976). They were loosely
inspired by notions of basic biochemical organization, and were
devised specifically to consider some issues in the spontaneous
emergence of life. The systems are, broadly speaking,
``artificial chemistries'', with notions of atoms, molecules, and
reactions between them (both catalysed and uncatalysed). There
is an explicit notion of space, albeit only
one-dimensional.
Holland discussed one particular 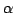 -universe in detail. In
this case, while (by design) no single molecular species would be
autocatalytic, it is trivially the case that an infinite class of
collectively autocatalytic networks can be instantiated.
This fact can be interpreted--in retrospect--as a specific
example of the results presented by Kauffman regarding the
relatively weak conditions which are needed for such a
phenomenon. Of course, Holland's results significantly predate
Kauffman's more general results, and are expressed in a
different vocabulary.
-universe in detail. In
this case, while (by design) no single molecular species would be
autocatalytic, it is trivially the case that an infinite class of
collectively autocatalytic networks can be instantiated.
This fact can be interpreted--in retrospect--as a specific
example of the results presented by Kauffman regarding the
relatively weak conditions which are needed for such a
phenomenon. Of course, Holland's results significantly predate
Kauffman's more general results, and are expressed in a
different vocabulary.
Holland's particular interest with this model system was to
assess the expected emergence time of instances of such
collectively autocatalytic networks. As it turns out,
these results are of limited value. Although the reaction
networks he cites are--abstractly--collectively autocatalytic,
they are not in fact capable of sustaining themselves under the
conditions envisaged by Holland (McMullin, 1992b).
This is at least in part due to the specific dynamics of the
system, including diffusion, and the occurrence of unanticipated
``side-reactions'' which were not allowed for in Holland's
analysis. There is also a significant effect due to rapid
depletion of the initial ``food set''.
It is possible (though, to my knowledge, no specific experiments
have been carried out) that at least some of the
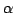 -universe reaction networks might be successfully
self-sustaining if the system were organized in the form of a flow
reactor (i.e., with a continuing inflow of food set materials).
However, regardless of that, this system actually does not
provide any mechanism for spatial localization or containment
which could be caused as a result of any reactions
instantiated in the system. Therefore we can say that, even if
it could be made to host a viable, self sustaining,
reaction network, multiple instances of the same network would
not be able to maintain their separation, but would
inevitably merge together and become indistinguishable.
-universe reaction networks might be successfully
self-sustaining if the system were organized in the form of a flow
reactor (i.e., with a continuing inflow of food set materials).
However, regardless of that, this system actually does not
provide any mechanism for spatial localization or containment
which could be caused as a result of any reactions
instantiated in the system. Therefore we can say that, even if
it could be made to host a viable, self sustaining,
reaction network, multiple instances of the same network would
not be able to maintain their separation, but would
inevitably merge together and become indistinguishable.
Therefore the 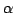 -universes are not capable of exhibiting
autopoietic agents, according to my heuristic test.
-universes are not capable of exhibiting
autopoietic agents, according to my heuristic test.
Tierra is a class of model system invented by Tom Ray
specifically to investigate evolution in an abstract
framework (Ray, 1992). The inspiration or
metaphor for the system is that of the Cambrian explosion. That
is, the primitive entities are intended to be analogous to
biological (rather than molecular) species; and the dynamics are
supposedly ecological and evolutionary rather than chemical.
However, I shall suggest that a chemical metaphor may be at least
equally applicable, and perhaps illuminating.
In practice, Tierra can viewed as a development of an
earlier line of systems, including Core Wars
(Dewdney, 1987) and Coreworld
(Rasmussen et al., 1990), with, indeed, some strong similarities to
the 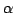 -universes already discussed. These all involve some
sort of one dimensional or linear spatial system, similar to a
conventional computer memory (the ``core'') in which are embedded
patterns that can effectively act as information processors or
(concurrent) computer programs. More technically, each
concurrently executing program is termed a separate
process. Given this general structure, one can
immediately envisage circumstances in which processes can
interact, can create new processes, and can be destroyed. On a
chemical metaphor this means taking individual processes as
molecules (with their programs defining their molecular
species), and their interactions as chemical reactions.
The conventional possibilities already raised here for self
sustaining systems thus arise afresh in this context.
-universes already discussed. These all involve some
sort of one dimensional or linear spatial system, similar to a
conventional computer memory (the ``core'') in which are embedded
patterns that can effectively act as information processors or
(concurrent) computer programs. More technically, each
concurrently executing program is termed a separate
process. Given this general structure, one can
immediately envisage circumstances in which processes can
interact, can create new processes, and can be destroyed. On a
chemical metaphor this means taking individual processes as
molecules (with their programs defining their molecular
species), and their interactions as chemical reactions.
The conventional possibilities already raised here for self
sustaining systems thus arise afresh in this context.
Ray's experiments can be briefly summarized--in the chemical
metaphor--as follows. It is possible, in the basic
Tierra system, to construct individually autocatalytic
molecules. These are moderately complex, and not capable of
spontaneous emergence. However, if the system is manually seeded
with such a molecule, it reacts rapidly to fill the reactor.
Experiments are conducted under flow conditions (there is an
outflow of molecules and an inflow of the ``food
set''--unallocated core memory in this case). A single
individually autocatalytic species can persist in the reactor for
an extended period in these circumstances. However, over time,
more ``efficient'' individually autocatalytic species tend to
successively emerge and displace each other. Efficiency here
essentially means reaction speed. More complex dynamics then
ensue. ``Parasites'' emerge, which are not individually
autocatalytic in isolation but have an autocatalytic pathway
which can be catalysed by fully autocatalytic ``host'' species, which are
already present. These parasites and their hosts thus form--in
my terms--a somewhat degenerate kind of collectively
autocatalytic set; degenerate because some of the species are
still individually autocatalytic. At later stages Ray reports
the emergence of what he terms ``sociality'', meaning entities
which ``can only replicate when they occur in aggregations''. In
my terms, it seems that these should be regarded as ``properly''
collectively autocatalytic, in that there are no longer any
individually autocatalytic components.
In these terms, Tierra can be regarded as again
independently corroborating Kauffman's results on the likely
spontaneous emergence of collectively autocatalytic reaction
networks--though with the addition of some significant and
interesting results on the subsequent development and even
elaboration of such networks. Ray himself does not make this
explicit connection, but that is presumably due, in part at
least, to his perspective of an ecological/evolutionary rather
than molecular metaphor.
However: again, as with the previous systems, Tierra
seems to lack any mechanism for spatial localization or
containment of collectively autocatalytic reaction networks. Note
carefully that this is true despite the fact that Ray variously
refers to ``organisms'', ``creatures'' and ``individuals'' in the
system; but what he means in each case is a single
Tierra process--i.e., the entity which, in my
terms, is analogous to a single molecule rather than a
self sustaining system. In particular, although these primitive
entities each have a specific, bounded, spatial extent in the
Tierra core, there is no sense in which they produce or
maintain this spatial boundary though their own
operations. On the contrary, Tierra enforces a
notion of ``memory allocation'' whereby some outside agency
allocates or reserves spatial segments of core to individual
processes, and this cannot be subverted by other processes. If
we consider the application of my heuristic test for autopoiesis
it again seems clear that multiple instances of the same reaction
network, inserted into the same Tierra reactor, would
not be able to maintain their separation; and thus,
Tierra is not capable of supporting fully autopoietic
organization.
Finally, let me turn to the SCL (Substrate-Catalyst-Link) system
(McMullin & Varela, 1997), which is a recent re-implementation of
the original computer model of autopoiesis
(Varela et al., 1974). It specifically corrected a defect in
the original published description of the model, establishing
that a previously undocumented interaction (chain inhibition) was
in fact essential to the autopoietic phenomenology of the model.
In any case, the experiments reported both in the original paper
and in this re-implementation were confined strictly to
examination of a single putatively autopoietic system, spatially
separated from any other. In this case, such an entity can
indeed exhibit a self-sustaining network, with a clearly
recognizable spatial structure or boundary which is both
maintained by, and in turn confines, the reaction network.
It is then interesting to enquire how this behaviour is affected
if two such entities are placed in close spatial proximity, as
envisaged in the heuristic test described above. (Since the SCL
system is deliberately simplified there is, in fact, only one
possible self sustaining reaction network; therefore the multiple
instances are necessarily instances of the same network).
Some (unpublished) experiments have been conducted along these
lines. The outcome is, at best, inconclusive. The details are
quite technical and only an outline will be presented here.
It should first be noted that the self sustaining agents in this
system are quite unstable, even in isolation (see the example
runs in McMullin & Varela 1997), which makes any interpretation
of results quite difficult. However, this instability does
seem to be exacerbated when multiple agents are in close
proximity. In particular, the chain inhibition interaction,
mentioned earlier as crucial to the operation of an isolated
agent, turns out to also have an unintended side effect of
inhibiting maintenance of the bounding membrane when two
membranes are adjacent to each other. This means that, if
anything, adjacent agents tend positively to merge rather
than to maintain their individuality.
On balance then, I would say that the self sustaining agents in
the SCL system do not pass my suggested heuristic test for
``full'' autopoiesis. This must be considered at least a little
controversial given that the model was designed explicitly to
illustrate autopoietic organization (albeit in minimal
form).
The primary purpose here has been to review and contrast the
notions of autopoiesis and collective autocatalysis. This has
resulted in a focus on the autopoietic requirement for spatial
localization or confinement to itself be a product of the
reaction network. I have attempted to make this criterion as
clear as possible by proposing a specific heuristic test. In
essence this says that the critical test should not merely
involve the ability of an entity to discriminate or demarcate
itself from some sort of relatively disorganized background.
Rather, it should require the ability for an agent to
discriminate itself from other, spatially adjacent, but
organizationally identical, agents. In particular,
although it is not an integral element of the autopoietic
concept, it seems to me that for agents to serve as actors in a
Darwinian selective process, it is essential that they should be
capable of this minimal ``individuation''.
In reviewing a number of abstract models of biological
organization, I have tried to bring out the fact that--as
envisaged by Kauffman--the emergence of collective autocatalysis
seems to be relatively easy or robust. Systems with wildly
different underlying architectures seem to exhibit this
phenomenon, corroborating the claim that the conditions for its
appearance are relatively weak. On the other hand, it seems that
none of these systems should qualify as exhibiting
properly autopoietic organization--including even the SCL system
which was specifically concepted as an exemplar of autopoiesis.
It is not clear to me whether this is merely because these
systems have not (with the obvious exception of SCL) been
designed with this end in mind; or because autopoietic
organization is, in fact, a fundamentally more elusive
phenomenon than collective autocatalysis. I would welcome
discussion on the question.
-
Dewdney, A. K. (1987),
- `Computer Recreations:
A Program Called MICE Nibbles its Way to Victory at the First Core Wars
Tournament', Scientific American 256(1), 8-11.
-
Eigen, M. & Schuster, P. (1979),
-
The Hypercycle: A Principle of Natural Self-Organization,
Springer-Verlag, Berlin.
-
Fontana, W. & Buss, L. W. (1994 a),
- ` ``The Arrival of the Fittest'': Toward a Theory of
Biological Organization', Bulletin of Mathematical Biology 56(1), 1-64.
-
Fontana, W. & Buss, L. W. (1994 b),
- `What would be Conserved if ``the Tape were Played
Twice''?', Proc. Natl. Acad. Sci. USA 91, 757-761.
-
Holland, J. H. (1976),
- Studies of the
Spontaneous Emergence of Self-Replicating Systems Using Cellular Automata and
Formal Grammars, in A. Lindenmayer & G. Rozenberg, eds,
`Automata, Languages, Development', North-Holland, New York, pp. 385-404.
-
Kauffman, S. A. (1993),
- The origins of
order: self-organization and selection in evolution, Oxford University
Press, Oxford.
-
Maturana, H. R. & Varela, F. J. (
1973),
- Autopoiesis: The Organization of the Living, in Autopoiesis and Cognition: The Realization of the Living
Maturana & Varela (1980), pp. 59-138.
Dated 1973. First published
1972 in Chile under the title De Maquinas y Seres Vivos, Editorial
Universitaria S.A.
-
Maturana, H. R. & Varela, F. J. (
1980),
- Autopoiesis and Cognition: The Realization of
the Living, Vol. 42 of Series: Boston Studies in the Philosophy of
Science, D. Reidel Publishing Company, Dordrecht, Holland.
With a preface to `Autopoiesis' by Stafford Beer. Series editors:
Robert S. Cohen and Marx W. Wartofsky.
-
McMullin, B. (1992a),
- Artificial
Knowledge: An Evolutionary Approach, PhD thesis, Ollscoil na hÉireann,
The National University of Ireland, University College Dublin, Department of
Computer Science.
http://www.eeng.dcu.ie/~alife/bmcm_phd/
-
McMullin, B. (1992b),
- The Holland
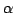 -Universes Revisited, in F. J. Varela & P. Bourgine,
eds, `Toward a Practice of Autonomous Systems: Proceedings of the First
European Conference on Artificial Life', Series: Complex Adaptive Systems,
MIT Press, Cambridge, pp. 317-326.
-Universes Revisited, in F. J. Varela & P. Bourgine,
eds, `Toward a Practice of Autonomous Systems: Proceedings of the First
European Conference on Artificial Life', Series: Complex Adaptive Systems,
MIT Press, Cambridge, pp. 317-326.
The preliminary results reported in this paper were subsequently
elaborated in much more detail in
(McMullin, 1992a, Chapter 5).
-
McMullin, B. & Varela, F. J. (1997)
- , Rediscovering Computational Autopoiesis, in P. Husbands & I. Harvey, eds, `Proceeedings of the Fourth European Conference on Artificial
Life', Series: Complex Adaptive Systems, MIT Press, Cambridge.
http://www.eeng.dcu.ie/~alife/bmcm-ecal97/
-
Rasmussen, S., Knudsen, C., Feldberg, R. & Hindsholm, M.
(1990),
- `The Coreworld: Emergence and
Evolution of Cooperative Structures in a Computational Chemistry', Physica 42D, 111-134.
-
Ray, T. S. (1992),
- An Approach to the
Synthesis of Life, in C. G. Langton, C. Taylor, J. D. Farmer
& S. Rasmussen, eds, `Artifical Life II', Vol. X of Series:
Sante Fe Institute Studies in the Sciences of Complexity, Addison-Wesley
Publishing Company, Inc., Redwood City, California, pp. 371-408.
-
Varela, F. J., Maturana, H. R. & Uribe, R. (
1974),
- `Autopoiesis: The Organization of Living Systems, its
Characterization and a Model', BioSystems 5, 187-196.
Acknowledgments
Some of the work mentioned here was carried out while I was a
visiting researcher with the Swarm Project
Group
at the
Santa Fe Institute. This visit
was made possible by generous support from Dublin City
University
and the Swarm Project. Swarm
has been supported by Grant No. N00014-94-1-G014 from the
Department of the Navy, Naval Research Laboratory, acting in
cooperation with the Advanced Research Projects Agency. Swarm has
also benefited from earlier support from The Carol O'Donnell
Foundation and from Mr. and Mrs. Michael Grantham.
The report was prepared at the kind invitation of Gertrudis Van
de Vijver, of the Research Community on Evolution and Complexity,
Fund for Scientific Research, Flanders.
All errors remain, of course, my own responsibility.
Revision History
First published in April 1999 as Technical Report
No. bmcm9901 of the Artificial Life
Laboratory
of Dublin
City University. First presented at the
workshop Closure: Emergent Organizations and their
Dynamics, May 3-5, 1999, University of Ghent, Belgium.
Author Contact Information
Barry
McMullin
Retrieval
The resources comprising this paper are electronically
retrievable, in various formats, via the World Wide Web, from:
Copyright
This report is copyright ©1999 by
Barry McMullin.
Permission is hereby granted to private individuals to access,
copy and distribute this work, for purposes of private study
only, provided that the distribution is complete and unmodified,
is accompanied by this copyright notice, and that no charges are
levied. The work may not be accessed or copied, in
whole or in part, for commercial purposes, except with the prior
written permission of the author.
All other rights reserved.
Footnotes
- ...Varela:Autopoiesis.1
- It has recently become clear
that the original published description of this model had a
significant technical defect; but that does not affect the
current discussion, and in any case, has now been corrected
(McMullin & Varela, 1997).
Copyright © 1999 All Rights Reserved.
Timestamp: 2003-03-28
mcmullin@eeng.dcu.ie
![]() -universes, Tierra, SCL).
-universes, Tierra, SCL).