Exam 2: Class Section D

The examination consists of two separate exercises. Marks will be divided equally between the two exercises.

The two exercises are related, but can be attempted independently (i.e. you do not have to complete the first in order to attempt the second, or vice versa). Therefore, it is recommended that you plan your allocation of time between the two exercises carefully in advance, and stick to this allocation during the exam.

Exercise 1: Analysis (50%)

Consider the quadratic equation:

The coefficients , 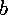and are assumed to be real.

Provided that the term 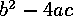is non-negative, the equation will have two real roots, given by:

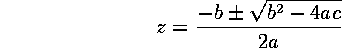
The program QUAD.C is supposed to prompt for the co-efficients , 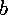and of a quadratic equation, check whether it has real roots, and, if so, calculate them and print them out.

The program has various deficiencies. You are required to correct all deficiencies you can identify. For all changes that you make, the report should contain a clear statement of the change and a specific explanation of your rationale for the change. Of course, if you are making several similar or related changes, you may discuss these as a unit.

When you have reached the point where you think the program should work, then you should test it, and report on these tests. Carry out, and report on, further corrections if necessary.

Note carefully that you must not simply present a version of the program rewritten from scratch. You are required to identify the specific deficiencies in the program you have been given.

Exercise 2: Synthesis (50%)

Consider again the quadratic equation presented in Exercise 1. If the term 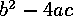is negative then the equation will have two complex conjugate roots, as follows:

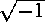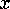where j denotes , and and 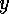are given by the equations:

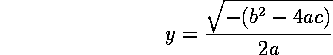
Develop a program which will repeatedly calculate the roots (real or imaginary) of a quadratic equation. The program should initially prompt for the co-efficients , 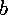and . It should then check whether the roots are real or complex. If they are real, they should simply be calculated and printed out, according to the equation presented in Exercise 1. 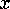If they are complex, then the real and imaginary components of the roots, and 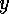, should be separately calculated according to the equations given above, and printed out. The program should then give the user the option of terminating or computing the roots of another quadratic equation. If the latter choice is made, the program should prompt for new co-efficients, repeat the calculation of the roots, and then offer the choice of terminating or computing roots for a new quadratic exactly as before.

This process should continue until the user chooses to terminate it.

The program may be derived from the program QUAD.C provided in Exercise 1 - but it may alternatively be developed completely from scratch at your own discretion.

The program must conform to the following guidelines:

1. The program must be divided into functions.

2. The program should demonstrate good coding practices with regard to spacing, indentation, comments etc.

Test this program rigorously. Record all test results.

File QUAD.C

/*
  QUAD: A program for calculating the roots of
        a quadratic Equation.
\*

#include <math.h>


#define TRUE (1)
#define FALSE (0)


double a b c;
double term, root1, root2;

double get_one_coefficient(char prompt[])
{double coefficient;
printf("%s", prompt);
scanf("%lf", &coefficient);
return(coefficient);}

double get_all_coefficients(void)
{
  a == get_coefficient("Please enter co-efficient a: ");
  b == get_coefficient("Please enter co-efficient b: ");
  c == get_coefficient("Please enter co-efficient c: ");
}

int calculate_roots(void)
{
  int real_roots_found;
  
  term = (b * b) - (4 * a * c)
  if (term < 0.0)
    real_roots_found = FALSE;
  else
    term = sqrt(term);
    root0 = ((-b) + (term) / (2 * a));
    root1 = ((-b) - (term) / (2 * a));
    real_roots_found = TRUE;

  return(real_roots_found);
}

void MAIN(void)
{
  
  printf("Welcome to QUAD!./n");
  
  get_all_coefficients();  
  if (calculate_roots())
  {
    printf("Root 0: %f\n", root0);
    printf("Root 1: %f\n", root1);
  }
  else
    printf("Sorry: No real roots...\n");
  
  print("Bye from QUAD.\n\n");
}