<b>floating_point_type</b>
Document: The safe-c User Guide
 string_type
string_type
 Constants and Data Types
Constants and Data Types
 integer_type
integer_type
Objects of floating_point_type may take on values representing
non-integer, rational, numbers. Internally these are
represented in so called floating point format. This is
somewhat like normal scientific notation - such as 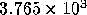 . That is, there is a mantissa (
. That is, there is a mantissa (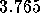 in this
example) and a separate exponent (
in this
example) and a separate exponent (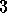 in this example).
The mantissa has a some finite range which, in effect, determines
the number of significant digits that can be represented. The
exponent also has a finite range which determines the maximum and
minimum absolute values which can be represented. Of course,
internally in the computer, both the mantissa and the exponent are
represented in binary notation; and the exponent is a power of 2
(normally) rather than a power of 10.
in this example).
The mantissa has a some finite range which, in effect, determines
the number of significant digits that can be represented. The
exponent also has a finite range which determines the maximum and
minimum absolute values which can be represented. Of course,
internally in the computer, both the mantissa and the exponent are
represented in binary notation; and the exponent is a power of 2
(normally) rather than a power of 10.
In the particular case of floating_point_type, the mantissa is
equivalent to approximately 15 decimal digits; and the exponent
is equivalent to approximately 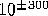 .
.
Constants of floating_point_type may be represented in your
programs in normal decimal notation, except that the decimal
point must be present, even if the fractional part is
intended as zero. Thus, 3.414 is a perfectly good
floating_point_type value, whereas 24 is not - it
would be interpreted as an integer_type value. If you
mean the floating_point_type value corresponding to the
number 24, then code it as 24.0 instead. Very large or
small floating_point_type constants can be represented using
scientific notation like this: -23.86e54 (for 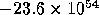 ) or 0.7433681e-123 (for
) or 0.7433681e-123 (for 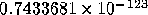 ).
).
Document: The safe-c User Guide
 string_type
string_type
 Constants and Data Types
Constants and Data Types
 integer_type
integer_type
McMullin@eeng.dcu.ie
Fri Jan 12 12:30:02 GMT 1996
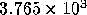 . That is, there is a mantissa (
. That is, there is a mantissa (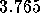 in this
example) and a separate exponent (
in this
example) and a separate exponent (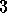 in this example).
The mantissa has a some finite range which, in effect, determines
the number of significant digits that can be represented. The
exponent also has a finite range which determines the maximum and
minimum absolute values which can be represented. Of course,
internally in the computer, both the mantissa and the exponent are
represented in binary notation; and the exponent is a power of 2
(normally) rather than a power of 10.
in this example).
The mantissa has a some finite range which, in effect, determines
the number of significant digits that can be represented. The
exponent also has a finite range which determines the maximum and
minimum absolute values which can be represented. Of course,
internally in the computer, both the mantissa and the exponent are
represented in binary notation; and the exponent is a power of 2
(normally) rather than a power of 10.
 string_type
string_type
 Constants and Data Types
Constants and Data Types
 integer_type
integer_type
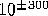 .
.
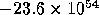 ) or 0.7433681e-123 (for
) or 0.7433681e-123 (for 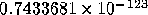 ).
).