This top-level step essentially scans each hole in the space, and permits each one to swap position with an immediately adjacent S, or with an S which can be reached through a single thickness of bonded L. As such, one might think that this step would be formally equivalent to scanning the S particles, and potentially moving them into neighboring holes. Furthermore, the latter would seem like a more consistent presentation, since the subsequent two top-level steps will be concerned with motion of free L and K particles respectively. However, as we shall see, it turns out that there are built in asymmetries between holes and S particles in this step, which prevent such an equivalent reformulation.
- 1.1. Form a list of the coordinates of
all holes
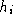 .
.
The notational convention here seems to be that h denotes the list of holes, and
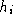 will then denote a
typical member of the list.
will then denote a
typical member of the list.
Presumably, an implementation may, for efficiency reasons, opt to maintain this list, rather than regenerate it afresh on each iteration.
It is not stipulated what the ordering of this list should be. This is a significant point, because subsequent substeps will process the members of the list in order; thus, regularities in the ordering of the list may possibly give rise to subtle unexpected (and unwanted) regularities in the movements of holes. It would therefore be preferable to stipulate that, whatever the ordering of the list as such, the subsequent processing steps should select elements in a random order, without repetition, until the list is exhausted (or, equivalently, that the list should be randomly permuted, on each timestep, before processing).
- 1.2. For each
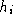 , make a random
selection,
, make a random
selection, 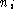 , in the range 1 through 4,
specifying a neighboring location.
, in the range 1 through 4,
specifying a neighboring location.
As previously outlined, a generalisation of the model would introduce a prior substep here, making motion of any given hole (or S particle?) occur only with some probability, say
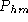 . Making
. Making 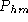 equal to 1 would then recover the exact algorithm
specified by Varela et al.
equal to 1 would then recover the exact algorithm
specified by Varela et al.
I presume that in this step, and in all similar subsequent cases, the intention is to use a uniform probability function over the specified event set.
The numbers 1 through 4 refer here to the neighborhood diagram (figure 1). Thus the selection is of an immediately neighboring position in one of the four orthogonal directions. The diagonally neighboring positions, 5 through 8, are not to be allowed or investigated. The reason for this is presumably that, as we shall see below, a subsequent refinement of this step will potentially investigate the positions one unit further away (the positions labeled 1' through 4'); such a ``two unit'' distant position, and especially the position ``in between'', will be unique in any of the orthogonal directions, but would be ambiguous for the diagonal directions. For simplicity of expressing the algorithm then, and without any serious loss of generality in the expected phenomenology, it is probably best just to restrict attention to the orthogonal directions.
- 1.3. For each
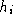 in turn, where
possible, move occupant of selected neighboring
location in
in turn, where
possible, move occupant of selected neighboring
location in 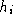 .
.
The way the algorithm has been organised here suggests that the intention is to first iterate over the entire list, selecting a candidate movement direction (step 1.2) and then, separately, iterate over the list again to actually make each move (step 1.3). However, it seems to me that this will be formally equivalent to iterating over the list just once, in each case picking a direction and then making the move before moving on to consider the next element. This would also be somewhat more efficient, so an implementation may presumably opt to prefer this approach.
The key phrase in this step seems to be ``where possible''. Two subsidiary steps or rules are now presented (1.31 and 1.32); since both of these stipulate conditions in which the movement should not be carried out (is not ``possible''), the intended interpretation seems to be that the motion is allowed except where 1.31 or 1.32 specifically disallow it.[7]
This is significant because (as we shall see) it implies that the movement will be carried out if the selected position contains any of an S, free L, or K particle. For that reason, this whole step is not symmetrical with respect to holes and S particles, and actually cannot be equivalently expressed in terms of S particles, as earlier suggested. However, since there are separate subsequent top-level steps (2 and 3) concerned explicitly with the motion of free L and K particles, it is doubtful whether the possibility of moving those particles in this step adds any significant functionality to the model. Further, by forcing the current top-level step to be expressed in terms of hole rather than S particle movement, this stipulation obscures the overall operation of the algorithm and introduces inconsistency with the expression of the other movement steps. Therefore, I suggest that it would have been preferable to explicitly exclude the possibility of free L or K particle movement in this step.[8]
- 1.31. If the neighbor is a hole or lies
outside the space, take no action.
If the neighbor position holds a hole then exchanging the particles would have no net effect on the overall configuration of the space. However, it is still good to make it explicit that these holes should not be swapped, as this will have some effect on the subsequent behaviour of the model. This is because, although the overall configuration of the space would be unchanged by this swap, the other hole may not yet have been processed through step 1--so moving it now would alter how it will be processed. Granted, it is doubtful whether this would have any substantial effect on the qualitative behaviour of the model; but it is surely simpler to simply rule it out, as 1.31 does.
The stipulation that, if the point is ``outside the space'' no further action should be taken, is useful, as it rules out the other possible behaviour one might consider, of choosing an alternative neighboring position and trying again.
- 1.32. If the neighbor
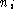 contains a
bonded L, examine the location
contains a
bonded L, examine the location 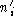 . If
. If 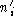 contains an S, move this S to
contains an S, move this S to 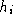 .
.
This captures the idea that an S particle can diffuse or permeate through a single layer of bonded link. However, it somewhat begs the question: if an S particle can permeate through a bonded L particle, why could it not permeate through a free L particle? The reason appears to be that, if a free L is found in the neighboring position then it is to be exchanged with the hole, rather than considering the possibility of an S particle beyond it. However, it has already been noted that incorporating free L particle movement into this part of the algorithm is questionable anyway; if the possibility of free L particle movement at this stage were dropped, then it would seem perfectly consistent (and even simpler) to permit S particles to permeate through a single thickness of both free and bonded L particles.
- 1.31. If the neighbor is a hole or lies
outside the space, take no action.
- 1.4. Bond any moved L, if possible
(Rules, 6).
This makes it clear that top-level section 6 is to be regarded as a sub-procedure.
The reference to ``any moved L'' again re-inforces the earlier interpretation of 1.3, that it is indeed intended to allow a hole to exchange positions with a free L, if one is encountered (despite the fact that free L particles will get an opportunity to move in top-level step 2 anyway).
Again, the layout of the algorithm suggests that there is to be a separate iteration over the (moved) free L particles, implementing the bond procedure, taking place after all the movements of 1.3 have been completed. This seems a little perverse from an implementation point of view, since it requires recording a list of the moved free L particles, to allow this separate iteration. It would seem simpler to just bond any moved free L when it is moved, rather than recording it for processing later, in a separate iteration. In the previous case of separate iterations (steps 1.2 and 1.3), I argued that the outcome would be formally equivalent if they were combined into a single iteration--and that therefore an implementation could opt to combine them. However, that argument does not carry through to the current case. It is evident that the ability of an L particle to form bonds depends on what other L particles are in its neighborhood. Therefore, the outcome of this bonding iteration will be potentially different depending on which L particle movements have been previously completed. Thus, it is not strictly free to an implementation to combine 1.4 into the same iteration as 1.3.
However, this does raise a more general criticism of the algorithm. As we shall see, there are single top-level steps concerned with realising the composition and disintegration reactions. These essentially iterate over each potential reaction site in the space, and permit one such reaction per timestep. One might have thought that the bonding reaction could (and, for consistency and simplicity, should) be implemented in essentially the same way. However, the bonding reaction is actually handled in a quite different manner. Instead of a single top-level step for bonding, there are two distinct sub-procedures (6 and 7), both concerned with the bonding reaction, but with quite different behaviours; of these, one is invoked in only one part of the algorithm (7 is invoked only as part of top-level step 5, i.e. following disintegration), and the other is repeatedly invoked in the other top-level steps. This certainly makes expected behaviour of the bonding reaction significantly more obscure, while also making the overall structure of the algorithm a good deal more complex. It is not at all clear what the rationale for this might have been. For example, it is possible that the particular implementation of bonding which was chosen had a significant effect on the qualitative phenomenology (and especially the emergence and stability of autopoietic structures); however, if that was the case, it would have been very helpful for this to be made explicit and elaborated in some detail.
This step is concerned with the movement of free L particles. It is significantly complicated by the idea of the various particle types having different ``masses'' and the possibility of ``displacements''. It also incorporates the possibility of bonding reactions, as with top-level step 1 (rather than deferring the bonding reaction to a single top-level step in its own right).
- 2.1. Form a list of the coordinates of free
L's,
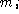 .
.
Again, the presumed notation here is that m denotes the list, and
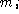 a typical element of the
list. However, whereas h was presumably mnemonic
for the list of holes formed in top-level step 1, there
is no apparent mnemonic intention here.
a typical element of the
list. However, whereas h was presumably mnemonic
for the list of holes formed in top-level step 1, there
is no apparent mnemonic intention here.
As with 1.1, the implementation may presumably opt to maintain this list rather than regenerating it; and, again, it would probably be preferable to randomly permute it before processing on each timestep, to guard against artifacts arising from any systematic ordering.
- 2.2. For each
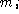 , make a random selection,
, make a random selection,
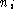 , in the range 1 through 4, specifying a
neighboring location.
, in the range 1 through 4, specifying a
neighboring location.
As with step 1.2, movement is allowed only in the four orthogonal directions.
- 2.3. Where possible, move the L occupying the
location
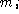 into the specified neighboring
location.
into the specified neighboring
location.
We interpret this, as with 1.3, as a general rule which will be qualified by the following subsidiary steps. That is, it is assumed that the move is possible, unless these substeps rule it out. Also, as with 1.2 and 1.3, we assume that 2.2 and 2.3 may be combined into a single iteration if there is some efficiency benefit in doing that.
- 2.31. If location specified by
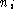 contains
another L, or a K, then take no action.
contains
another L, or a K, then take no action.
As with a hole swapping with a hole, a free L particle swapping with a free L particle would have no net effect on the overall configuration of the space; but again, it could have an effect on the behaviour of the model, because the other free L might not yet have been processed for movement, and would be subsequently processed differently if it is moved now. So it does seem worthwhile to explicitly exclude this.
The rule does imply two other significant conditions. First that an L particle will not swap with a K particle. This is presumably intended to partially reflect the idea that K is of greater ``mass'' than L; but it is somewhat inconsistent, because K particles can swap with the (zero ``mass''?) holes in step 1. The second condition implied here is that a free L particle will not swap positions with a bonded L particle. This reflects the general stipulation that bonded L particles are absolutely immobile.
- 2.32. If location specified by
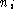 contains an S, the S will be displaced.
contains an S, the S will be displaced.
This step attempts to capture the idea that because an L particle is of greater ``mass'' than an S particle, then it can ``displace'' the S particle to some other position, thus making a hole that the L can then move into. However, the details are necessarily somewhat complex, because there may be some difficulty in actually displacing the S. This is detailed in the following three steps, subsidiary to 2.32, which attempt to explain exactly how this idea of ``displacement'' is to be realised.
- 2.321. If there is a hole adjacent to the S, it
will move into it. If more than one such hole,
select randomly.
- 2.322. If the S can be moved into a hole by
passing through bonded links, as in step 1, then it
will do so.
Presumably, 2.322 is intended as a fallback, only to be applied if the S particle cannot be moved in accord with 2.321.
The phrase ``as in step 1'' deserves some elaboration. The intention is evidently that the S particle is allowed to exchange with a hole which is behind a single thickness of bonded L particles. However, whereas in step 1, a single direction (out of four) is first chosen, and the S particle is either moved in that direction or not at all, the intention here seems to be that all directions (three only) should be assessed for this possibility;[9] and if more than one is possible, select one at random. I take this interpretation, even though it is not fully stated, for consistency with the immediately prior step, 2.321, and because the next step (2.323) explicitly refers to the case that ``the S cannot be moved into a hole'', implying that every possible way of ``displacing'' the S should be checked first.
Thus, although 2.322 does involve some similarity to step 1, there are significant differences also (especially that fact that step 1 was centered on a hole not an S particle, the fact that all available directions are tried rather than plumping for one only, and the fact that only three directions, at most, might be possible). This is of interest in that it effectively rules out any idea of isolating this functionality into a single sub-procedure, shared both by step 1 and step 2.322.
- 2.323. If the S cannot be moved into a hole, it
will exchange locations with the moving L.
This is the final fallback case: in essence, if the S particle cannot actually be ``displaced'', then the free L particle will simply swap positions with it.
- 2.321. If there is a hole adjacent to the S, it
will move into it. If more than one such hole,
select randomly.
- 2.33. If the location specified by
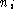 is a
hole, then L simply moves into it.
is a
hole, then L simply moves into it.
We can note again that, since an L particle can swap position with a hole at this step anyway, it is questionable what purpose is served by allowing equivalent swaps in step 1 also.
Note that steps 2.31 through 2.33 have actually enumerated all possible contents of the neighbor position, and specified a corresponding behaviour. These rules were ordered (roughly) as K, L, S, and finally hole. It might have been somewhat more clear to order them with hole before S, since this would get the simpler cases out of the way before dealing with the cumbersome case of S. In any case, from an implementation point of view, it is clear that these cases are mutually exclusive, and can thus be considered in any desired order.
- 2.31. If location specified by
- 2.4. Bond each moved L, if possible.
As with 1.4, the bonding reaction has been inserted as a subprocedure invocation here. Unfortunately, there are two top-level steps concerned with bonding--6 and 7--so it is not immediately clear which should be invoked in this case. However, as we shall see, step 6 expects an argument of the position of a free L particle, whereas step 7 apparently expects the position where a free L has just disintegrated. Therefore, it may be assumed that the intention is to invoke top-level step 6 as the subprocedure here.
Similar criticisms of the overall approach to the bonding reaction as detailed under step 1.4 apply again here. One additional point is worth making explicit now: because the possibility of a bonding reaction is being reevaluated here, certain free L particles may be assessed for bonding more than once in any given timestep (because they happen to be moved in, say, both steps 1 and 2), whereas others will not. This seems a rather arbitrary variability in reaction rate, which would be better avoided.
This is primarily concerned with movement of K particles. As with top-level step 2, it is significantly complicated by the idea of the various particle types having different ``masses'' and the possibility of ``displacements''; however, the situation is even more complex this time, as the K particle may displace a free L particle which must (first) displace a S particle. This step also allows for movement and potential bonding of free L particles, even though possibilities for both these actions have already been allowed in both the previous top-level steps.
- 3.1. Form a list of the coordinates of
all K's,
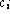 .
.
Again, the presumed notation here is that c denotes the list, and
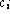 a typical element of the list.
c is presumably mnemonic for ``catalyst''--though
for consistency, it would have been preferable either
to use k, or use C as the code for the
catalyst particle.
a typical element of the list.
c is presumably mnemonic for ``catalyst''--though
for consistency, it would have been preferable either
to use k, or use C as the code for the
catalyst particle.
As with 1.1, and 2.1, the implementation may presumably opt to maintain this list rather than regenerating it; and, again, it would probably be preferable to randomly permute it before processing on each timestep, to guard against artifacts arising from any systematic ordering.
- 3.2. For each
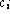 , make a random
selection
, make a random
selection 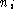 , in the range 1 through 4,
specifying a neighboring location.
, in the range 1 through 4,
specifying a neighboring location.
As with step 1.2 and 2.2, movement is allowed only in the four orthogonal directions.
- 3.3. Where possible, move the K into the
selected neighboring location.
We interpret this, as with 1.3 and 2.3, as a general rule which will be qualified by the following subsidiary steps. That is, it is assumed that the move is ``possible'', unless these substeps rule it out. Also, as with 1.2 and 1.3, and 2.2 and 2.3, we assume that 3.2 and 3.3 may be combined into a single iteration if there is some efficiency benefit in doing that.
- 3.31. If the location specified by
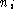 contains a BL or another K, take no action.
contains a BL or another K, take no action.
As with a hole swapping with a hole (step 1.31), or a free L particle swapping with a free L particle (step 2.31), a K particle swapping with a K particle would have no net effect on the overall configuration of the space; but again, as with those previous two cases, it could have an effect on the behaviour of the model, because the other K might not yet have been processed for movement, and would be subsequently processed differently if it is moved now.
This rule also incorporates the condition that a K particle will not swap positions with a bonded L particle, again reflecting the general stipulation that bonded L particles are absolutely immobile.
- 3.32. If the location specified by
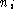 contains a free L, which may be displaced according
to the rules of 2.3, then the L will be moved, and
the K moved into its place. (Bond the moved L, if
possible).
contains a free L, which may be displaced according
to the rules of 2.3, then the L will be moved, and
the K moved into its place. (Bond the moved L, if
possible).
This step seems straightforward, essentially invoking step 2.3 as a subprocedure. However, there is a difficulty, or ambiguity with this. Step 2.3 was designed to assess the possibility of moving a free L particle in one, pre-specified or chosen, direction only. It is not at all clear that the same applies to the current case. It is possible that the intention is to try to displace the free L particle in the same direction as the attempted move of the K particle (
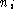 in the context of
3.32). However, that would be somewhat inconsistent
with the policy specified in 2.321 where an S
particle, being displaced by a free L particle,
may move in any available direction.
Furthermore, as we shall see, step 3.34 will specify
a ``fallback'' action for the case that the free
L particle is ``not movable by rules 2.3'',
which suggests to me that the current step (3.32) is
intended to attempt all possible directions of
movement for the free L particle. In any case,
whatever the ``correct'' interpretation, the rule, as
stated, is certainly ambiguous.
in the context of
3.32). However, that would be somewhat inconsistent
with the policy specified in 2.321 where an S
particle, being displaced by a free L particle,
may move in any available direction.
Furthermore, as we shall see, step 3.34 will specify
a ``fallback'' action for the case that the free
L particle is ``not movable by rules 2.3'',
which suggests to me that the current step (3.32) is
intended to attempt all possible directions of
movement for the free L particle. In any case,
whatever the ``correct'' interpretation, the rule, as
stated, is certainly ambiguous.
This rule also parenthetically mentions that, if the free L particle is moved, it should be bonded. As in step 2.4, the bonding sub-procedure has not been stipulated explicitly, but it seems clear that top-level step 6 is intended.
Note that the invocation of bonding at just this point in the algorithm is actually inconsistent with the way it was handled at steps 1.4 and 2.4. In the previous cases, all free L particle movements were completed before any were processed for bonding. Whereas, in the current case, the possibility of bonding is considered as each free L particle is moved, rather than as a separate iteration. This change in bonding procedure or policy is repeated in step 3.34; but then, in top-level step 4, we shall see a reversion to the same policy as steps 1 and 2, where bonding is deferred to the end of the (top-level) step. There is no apparent rationale for this variation in policy. It further re-inforces the arguments made earlier that the bonding reaction should be processed just once, as a top-level step of its own.
- 3.33. If the location specified by
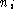 contains an S, then move the S by the rules of
2.32.
contains an S, then move the S by the rules of
2.32.
Again, this looks like 2.32 should be simply invoked, in effect, as a sub-procedure; but again, there is a difficulty with this. Step 2.323--being part of 2.32--covers the case where it turns out that the S particle cannot be displaced, and stipulates that the S particle will then ``exchange locations with the moving L''. The problem is that, in the context of 3.33, there is no ``moving L'', but rather a ``moving K''. Of course, the intended meaning here is clear enough; but to express it cleanly, step 2.3 ought to be explicitly separated out as a subprocedure, and given an argument, being the position of an indefinite particle (actually either a free L or a K--but the subprocedure will be oblivious to this) which is trying to displace it.
- 3.34 If the location specified by
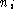 contains a free L, not movable by rules 2.3,
exchange the positions of the K and the L. (Bond L
if possible).
contains a free L, not movable by rules 2.3,
exchange the positions of the K and the L. (Bond L
if possible).
This is analogous to step 2.323.
However: since it is essentially a fallback, or alternative, to step 3.32, it would preferable if it came immediately after 3.32; or, for consistency with the way 2.32 was expressed, 3.32 and 3.34 could have been made subsidiary cases of a single rule. In any case, as the various substeps of 3.32 are mutually exclusive, it will be open to an implementation to re-order the consideration of them if convenient.
- 3.35. If the location specified by
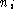 is a hole, the K moves into it.
is a hole, the K moves into it.
A similar comment applies as at step 2.33. Given that this step allows a K particle to exchange with a hole, it seems unnecessary to allow for that at top-level step 1 also.
In closing top-level step 3, we may finally note that, unlike top-level steps 1 and 2, there is no final step here concerned with bonding any moved link--because the bonding was integrated into substeps 3.32 and 3.34, as already discussed.
- 3.31. If the location specified by
This step implements the reaction earlier termed ``composition'' but now (apparently) renamed ``production''. This is specified to occur only under the influence of K particles; therefore it is efficient to focus only on those positions in the space where there are such particles, and iterate over each in turn. Each particle can trigger at most one production reaction per timestep. To do so, there must be two S particles immediately adjacent both to the K particle and to each other (in this case, diagonal neighbors are counted as immediately adjacent). If there are multiple adjacent pairs of S particles, adjacent to a single K particle, one is chosen at random, as the reacting pair. The reaction proper is then implemented by deleting the two S particles, and replacing them by a single L particle. This is located randomly at either of the two positions previously occupied by the S particles (the other position becoming a hole). Finally, the possibility of bonding is processed for the newly created L particle (and, again, I would argue that it would be better for this to be handled as a single, separate, top-level step, rather than conflated with the production reaction).
As the algorithm is currently specified, if it is possible to carry out a production reaction in the neighborhood of a given K particle, then the reaction will happen. As previously discussed, this could instead be made subject to a reaction rate parameter (probability of reaction), to add an additional degree of flexibility to the range of models that could be investigated.
- 4.1. For each catalyst
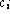 , form a list
of the neighboring positions
, form a list
of the neighboring positions 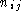 , which are
occupied by S's.
, which are
occupied by S's.
Strangely, this top-level step does not start with an explicit instruction to ``form a list of the coordinates of all K's,
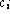 '', even though that is
clearly implied, and such an instruction was made
explicit in each of the previous top-level steps.
'', even though that is
clearly implied, and such an instruction was made
explicit in each of the previous top-level steps.
In any case, the same comments should be noted as in each of the previous such cases: it may be convenient, for implementation efficiency, to maintain this list rather than regenerate it; and, to avoid any artifacts arising from the order of this list, it should be randomly permuted before processing the production reaction.
Steps 4.1 through 4.3 are now interpreted as, in effect, substeps to be repeated for each K particle in the space.
Step 4.1 is simply concerned with identifying or listing the positions of S particles adjacent to each K particle. As step 4.1 is phrased, it reads as an instruction to form these lists (
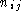 ) for all K particles
before proceeding to carry out the production
reactions for any of them. One might immediately
assume, as in the previous somewhat similar
cases[10], that it is free to the
implementation to choose to combine these two
iterations into one. However, the situation in this
case is actually more complex, and there is no real
choice; despite the phrasing of 4.1, these two
iterations surely must be combined into one.
The reason is that a given S particle may
be (initially) adjacent to more than one K
particle. If the lists
) for all K particles
before proceeding to carry out the production
reactions for any of them. One might immediately
assume, as in the previous somewhat similar
cases[10], that it is free to the
implementation to choose to combine these two
iterations into one. However, the situation in this
case is actually more complex, and there is no real
choice; despite the phrasing of 4.1, these two
iterations surely must be combined into one.
The reason is that a given S particle may
be (initially) adjacent to more than one K
particle. If the lists 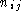 are all generated
first, before any of the production reactions are
carried out, then ``early'' production reactions may
actually render some of the ``later'' lists
invalid--because an S particle that was listed
as adjacent to a certain K particle has actually,
in the interim, reacted to give an L particle
under the action of a different K particle.
are all generated
first, before any of the production reactions are
carried out, then ``early'' production reactions may
actually render some of the ``later'' lists
invalid--because an S particle that was listed
as adjacent to a certain K particle has actually,
in the interim, reacted to give an L particle
under the action of a different K particle.
Of course, it is possible that the algorithm is ``correct'' as stated--in the sense that the authors actually did intend separate iterations to be used, and had not recognised the potential difficulty this could lead to. Provided the density of catalysts is ``low'', the probability of encountering this problem will also be low. The actual implementation run illustrated in (Varela et al. 1974) shows only a single K particle in the space--and, in that case, of course, the difficulty identified here cannot actually arise. However, it is a real defect in the algorithm, nonetheless; so I recommend that any new implementation should choose to combine the iterations, as outlined. It is apparent that this combination should make no difference to the effect on the space except in the case that the reactions at different K sites would interact--and for those cases, one needs the robust form of the algorithm.
- 4.11. Delete from the list of
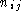 all positions for which neither adjacent neighbor
position appears in the list (i.e., ``1'' must be
deleted from the list of
all positions for which neither adjacent neighbor
position appears in the list (i.e., ``1'' must be
deleted from the list of 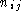 's, if neither 5
nor 6 appears, and a ``6'' must be deleted if
neither 1 nor 2 appears).
's, if neither 5
nor 6 appears, and a ``6'' must be deleted if
neither 1 nor 2 appears).
The numbers here refer, of course, to the neighborhood diagram presented earlier (figure 1).
Essentially what is happening here is that the original list,
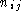 contained all S particles
immediately adjacent to the given K particle
(
contained all S particles
immediately adjacent to the given K particle
( 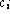 ), whereas production is possible only for S
particles that come in pairs--i.e. that are
adjacent both to each other and to the K particle.
Presumably, it is free to an implementation to generate
this ``reduced'' list ``directly''--rather than first
generating a list of all adjacent S particles and
then removing some elements from it again. In any
case, it is not at all clear why this step is expressed
as a sub-step of step 4.1. There are no
additional such sub-steps; it would seem that 4.11
could either have been made a separate step at the same
level as 4.1, or 4.1 and 4.11 could have been combined
into a single step.
), whereas production is possible only for S
particles that come in pairs--i.e. that are
adjacent both to each other and to the K particle.
Presumably, it is free to an implementation to generate
this ``reduced'' list ``directly''--rather than first
generating a list of all adjacent S particles and
then removing some elements from it again. In any
case, it is not at all clear why this step is expressed
as a sub-step of step 4.1. There are no
additional such sub-steps; it would seem that 4.11
could either have been made a separate step at the same
level as 4.1, or 4.1 and 4.11 could have been combined
into a single step.
- 4.11. Delete from the list of
- 4.2. For each
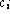 with a non-null list
of
with a non-null list
of 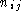 , choose randomly one of the
, choose randomly one of the 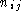 ,
let its value be
,
let its value be 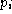 , and at the corresponding
location, replace the S by a free L.
, and at the corresponding
location, replace the S by a free L.
Again, the way this is phrased, it suggests a separate iteration over the K particles, but this is not a reasonable interpretation for the reason already explained.
The essential point of step 4.2 is to say that if there are multiple candidate pairs of S particles which may react under a given K, then one should be picked ``at random''. This does not mean exactly ``uniformly'' at random, because the choice is made in two stages. Instead of explicitly listing all possible pairs and then (say) choosing with a uniform distribution over them, the rule says to first pick a single (eligible) S particle and then two subsidiary steps (4.21 and 4.22) will deal with the issue of picking the second S particle to pair with this one. This can slightly skew the probability distribution among the possible pairs. For example, with four adjacent particles, the probability of choosing either end pair will be 3/8 versus 1/4 for the middle pair. On the other hand, the algorithm, as stated, does have the effect of ensuring that which S particle gets replaced with a free L is uniformly chosen from the candidates (whereas, if a pair was first picked with a uniform probability function, and then one position out of the pair chosen uniformly to be replaced by the L, this could skew the probability of locating the L particle somewhat in favour of the ``inner'' S particle locations).
In any case, it seems highly unlikely that these relatively fine distinctions in probability distribution for the production reaction would have any substantive effect on the qualitative phenomenology of the system.
- 4.21. If the list of
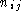 contains
only one which is adjacent to
contains
only one which is adjacent to 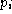 , then remove
the corresponding S.
, then remove
the corresponding S. - 4.22. If the list of
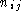 includes
both locations adjacent to
includes
both locations adjacent to 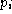 , randomly select
the S to be removed.
, randomly select
the S to be removed.
- 4.21. If the list of
- 4.3. Bond each produced L, if possible.
The disintegration reaction is superficially very
straightforward: each L particle (bonded or
otherwise) is considered for disintegration with a
probability ![]() , where
, where ![]() is an explicit parameter
of the model chemistry. However, as we shall see, there
is considerable complexity involved in actually
carrying out the disintegration.
is an explicit parameter
of the model chemistry. However, as we shall see, there
is considerable complexity involved in actually
carrying out the disintegration.
- 5.1. For each L, bonded or unbonded,
select a random real number, d, in the range
(0,1).
As with top-level step 4, there is presumably an implied prior step here, of forming a list of L particles; again, we assume that an implementation may opt to maintain this list instead of generating it anew each timestep; and, to avoid artifacts arising from the ordering, the list should be permuted before proceeding with the disintegration processing.
Again, the phrasing of step 5.1 seems to imply a separate iteration, generating a random number for each L particle, before coming back and processing the disintegration reaction. However, unlike the previous such cases, the notation here has changed subtly: the step refers to a single random number d, rather than a list,
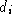 . That may suggest that, on this occasion,
a separate iteration to first generate the random
numbers is not intended. This is perhaps
supported by the fact that the rest of this top-level
step consists of only two sub-steps of
5.1--suggesting that they form part of the same,
single, iteration over the L particles. In any
case, there seems to be no formal distinction between
using a single iteration to both generate the random
numbers and process the disintegrations or using two
separate iterations--so this choice is presumably free
in the implementation.
. That may suggest that, on this occasion,
a separate iteration to first generate the random
numbers is not intended. This is perhaps
supported by the fact that the rest of this top-level
step consists of only two sub-steps of
5.1--suggesting that they form part of the same,
single, iteration over the L particles. In any
case, there seems to be no formal distinction between
using a single iteration to both generate the random
numbers and process the disintegrations or using two
separate iterations--so this choice is presumably free
in the implementation.
- 5.11. If
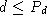 (
( 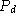 an
adjustable parameter of the algorithm), then remove
the corresponding L, attempt to re-bond (Rules, 7).
an
adjustable parameter of the algorithm), then remove
the corresponding L, attempt to re-bond (Rules, 7). - 5.12. Otherwise proceed to next L.
The effect of 5.1 combined with 5.11 and 5.12 is to say that each L particle should be subject to disintegration with probability
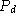 . This choice can
be achieved in the manner specified (i.e. by indirectly
using a sample of a uniform random variable); however, I
presume that if an implementation has a source of
bernoulli random variables, with programmable
probability, that may be substituted here instead.
. This choice can
be achieved in the manner specified (i.e. by indirectly
using a sample of a uniform random variable); however, I
presume that if an implementation has a source of
bernoulli random variables, with programmable
probability, that may be substituted here instead.
In any case, the real complexities of this reaction come into play in the case that a given L is, indeed, to be subject to disintegration (step 5.11).
There are two problems or difficulties to be considered.
Firstly, if the L particle was bonded, what should happen to those bonds? The obvious answer would be that they should simply be destroyed. However, the algorithm specifies something much more complex. Instead of simply destroying existing bonds, the algorithm specifies than an attempt must be made to ``re-bond''. The details of this are contained in a separate top-level step (7). The implication is that step 7 is to be regarded as a subprocedure. However, given that this is the only place where this subprocedure is invoked, it might have been simpler to include it as an explicit part of top-level step 5 instead.
Much more seriously, the ``re-bonding'' procedure is actually concerned not with destroying whatever bonds were associated with the disintegrated L particle--that is actually left implicit--but with forming new bonds among whatever L particles remain in the neighborhood of the disintegration site. In effect, this is therefore a special purpose variant of the bonding reaction.
As already discussed at length, there is no clearly articulated reason why the bonding reaction should be handled in such a complex way, conflated into the other reactions, rather than dealt with once per timestep in its own right. The current case is particularly troublesome because disintegration is the way that an autopoietic entity may be disrupted; if the autopoietic phenomenon is robust, one would not expect to have to insert special measures relating specifically to the reactions arising from such disruption. Yet, prima facie, it appears that just such special measures have been built into the algorithm here with this notion of ``rebonding''. As a further ancillary point: rebonding is actually specified to be invoked here regardless of whether the original L particle was previously bonded or not; again, this further serves to obscure the operation of the bonding reaction in general, providing yet another separate opportunity for bonding to happen per timestep. In any case, detailed consideration of rebonding will be deferred to the discussion of step 7 proper below.
The second outstanding difficulty with disintegration is that this reaction involves replacing a single L particle with two S particles. One of these will clearly occupy the position formally occupied by the L particle--but where is the other to be positioned? Presumably, it should be located in a hole--but that raises the non-trivial question of which hole? The algorithm gives absolutely no guidance here--it merely states categorically that, if
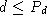 then the disintegration will take place.
then the disintegration will take place.
For chemical ``plausibility'' one would expect to choose a ``neighboring'' hole. Therefore, one might formulate a rule such as: if there is a hole immediately adjacent to the disintegration site, locate the extra S particle here; if there is more than one such hole, choose one uniformly at random. But what if there is no adjacent hole? In the general case, it may actually be necessary to scan arbitrarily far away to locate a hole.[11] Scanning arbitrarily far away from a reaction site, within a single timestep, clearly violates the basic idea of local interaction, which seems to be essential to the idea of a model ``chemistry'' of any sort, and should not be introduced without some clear rationale. Indeed, if I were developing this algorithm from scratch, I would suggest that the appropriate rule would be that, if there is no immediately adjacent hole, the disintegration should simply not occur. I doubt very much whether this would significantly affect the qualitative phenomenology. Alternatively, and more radically, I noted earlier that there was no clear requirement for the production reaction to require two S particles anyway; if the reaction were redefined so that a single S could be transformed to a single L particle (and vice versa for disintegration) then this whole difficulty would disappear anyway.
Nonetheless, we must record that a strict interpretation of the original algorithm appears to require searching arbitrarily far from the reaction site, until a hole is located. It appears to be entirely free to the implementation to decide all details of this search.[12]
- 5.11. If
This step must be given the coordinates of a free L.
This is the (main) subprocedure for implementing the bonding reaction. As already noted, it is invoked from each of the top-level steps 1 through 4. In each such case, there is a specific free L particle relative to which bonding will be attempted. I will refer to this below as the target L particle.
There are two imposed constraints on bonding. Firstly,
any given L particle can have at most two bonds.
Secondly, a second bond can form at any singly
bonded L particle only if the angle between it and
the prior bond will be at least ![]() . This bond
angle is illustrated in
figure 2 (redrawn from
figure 4 of the original paper). Note that this
diagram clearly indicates that diagonal bonds
are allowed in general, subject only to the
condition that a bond angle of
. This bond
angle is illustrated in
figure 2 (redrawn from
figure 4 of the original paper). Note that this
diagram clearly indicates that diagonal bonds
are allowed in general, subject only to the
condition that a bond angle of ![]() is not permitted.
is not permitted.
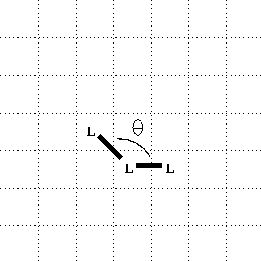
Figure 2: Definition of Bond-Angle ![]() .
.
One presumes that the rationale for disallowing
bond angles less than ![]() (i.e. either
(i.e. either
![]() , or the degenerate case of
, or the degenerate case of ![]() )
is to encourage the formation of more
``open'' chains; however, this is not discussed in
detail in the paper. It is difficult to judge how
significant it may be for the qualitative
phenomenology. In any case, one would like any
implementation to make it easy to relax this constraint
if desired.
)
is to encourage the formation of more
``open'' chains; however, this is not discussed in
detail in the paper. It is difficult to judge how
significant it may be for the qualitative
phenomenology. In any case, one would like any
implementation to make it easy to relax this constraint
if desired.
Bond formation, where possible, is ``forced''. That is, there is no ``reaction rate parameter'', or overriding probability, governing bond formation. Such a parameter could be added; but its effect would be seriously complicated by the fact that any given L particle might be considered (directly or indirectly) for bonding several different times within one timestep.
In outline, the strategy here is to first preferentially form bonds between the target L particle and neighboring L particles that already have one bond; if the target L particle is then still not fully bonded (i.e. does not yet have two bonds) then further bonding will be attempted with neighboring free L particles. In any case, the given L particle will be fully bonded, if that is possible. Wherever there are multiple possibilities, choices are made randomly (presumably uniformly among the possibilities). However, because of the multitude of possible neighborhood configurations, the algorithm for achieving all this is quite complex.
The flow of control through this procedure is particularly hard to follow. It seems important to note that, in contrast to earlier cases, the sub-steps in the part of the algorithm specify additional sequential steps, rather than providing clarification or constraints on the higher level, containing step.
Again, no specific rationale is offered for preferentially bonding to singly bonded L particles; but I speculate that this was intended to make the repair of a ruptured chain more likely or robust.
- 6.1. Form a list of the neighboring
positions
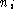 , which contain free L's, and the
neighboring positions
, which contain free L's, and the
neighboring positions 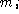 which contains singly
bonded L's.
which contains singly
bonded L's. - 6.2. Drop from the
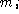 any which would
result in a bond angle less than
any which would
result in a bond angle less than 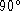 . (Bond
angle is determined as in Figure [2]).
[Figure 4 of the original.]
. (Bond
angle is determined as in Figure [2]).
[Figure 4 of the original.]
The ``bond angle'' here must be that formed at the neighboring, already singly bonded, L particle (in some position
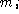 )--since any one
of these particles would only specify a single bond
to the target free L, and would thus not serve
to specify a bond angle at the target L.
)--since any one
of these particles would only specify a single bond
to the target free L, and would thus not serve
to specify a bond angle at the target L. - 6.3. If there are two or more of the
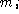 , select two, form the corresponding bonds,
and exit.
, select two, form the corresponding bonds,
and exit.
This expresses the preferred outcome: if possible, the free L particle should form its two bonds with two neighboring, singly bonded, L particles.
However, there is a difficulty with the algorithm as so far expressed. Consider, for example, the configuration shown in figure 3. The two neighboring, singly bonded particles are each separately eligible to form a bond with the target particle (neither such bond would generate a
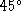 bond angle at the neighboring particle); but if
both bonds are formed, this will result in a
bond angle of
bond angle at the neighboring particle); but if
both bonds are formed, this will result in a
bond angle of 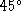 at the target L particle,
which presumably should not be allowed.
at the target L particle,
which presumably should not be allowed.
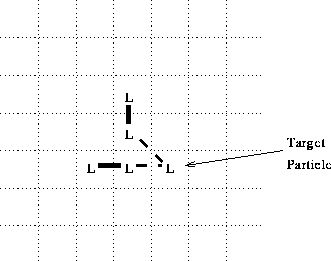
Figure 3: Scenario for formation of bad bond angle.
I suggest that the ``correct'' (or at least, non-defective) procedure in this case would be as follows. First, pick one of the
 (uniformly) at
random, and form the corresponding bond. Remove that
(uniformly) at
random, and form the corresponding bond. Remove that
 from the list m, and also any other position(s)
that would now result in a bond angle of
less than
from the list m, and also any other position(s)
that would now result in a bond angle of
less than 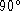 at the target particle (because the target
particle is, by now, singly bonded, this is a
well-defined constraint). If the list m is not now
empty, pick another
at the target particle (because the target
particle is, by now, singly bonded, this is a
well-defined constraint). If the list m is not now
empty, pick another 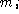 (uniformly) at random, form
the corresponding bond, and exit; but if the list m
is empty, attempt to form a second bond with a
neighboring free L particle (the precise
procedure for this will be specified in substeps 6.41
through 6.43).
(uniformly) at random, form
the corresponding bond, and exit; but if the list m
is empty, attempt to form a second bond with a
neighboring free L particle (the precise
procedure for this will be specified in substeps 6.41
through 6.43). - 6.4. If there is exactly one
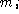 , form
the corresponding bond.
, form
the corresponding bond.
Given my reformulation of step 6.3, step 6.4 could now be collapsed into it (6.3 would then begin ``If the list m is non empty...''). However, the substeps 6.41 through 6.43 are still required, to deal with the situation of attempting to form a second bond with a neighboring free L particle. This set of steps is actually invoked from two possible points (within 6.4 and 6.61); thus it is effectively used as a subprocedure, and might have been better explicitly separated out as such. In any case, note carefully that the scenario on entry to substep 6.41 is always that the target particle is now singly bonded, and an attempt is being made to form a second bond to a neighboring free L particle; it will follow that the overall bonding procedure (top-level step 6) will definitely terminate somewhere within substeps 6.41 through 6.43. To put that another way, if control reaches substep 6.41, it will not subsequently proceed to step 6.5 or following steps. 6.5 is invoked only if the list m becomes empty without any bonds having been formed with the target particle.
- 6.41. Remove from the
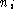 any which
would now result in a bond angle of less than
any which
would now result in a bond angle of less than
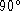 .
. - 6.42. If there are no
 , exit.
, exit.
In this case, the target particle must be left just singly bonded.
- 6.43. Select one of the
 , form the
bond, and exit.
, form the
bond, and exit.
In this case, two bonds have been formed with the target particle.
- 6.41. Remove from the
- 6.5. If there are no
 , exit.
, exit.
As already noted, control reaches this point only in the case that the list m is empty and the target L particle still has no bonds (it is still free). In that case we try to form an initial bond with an neighboring free L particle. Step 6.5 covers the case that there are no neighboring free L particles; in which case there is nothing further to try, and the target particle must be left free.
- 6.6. Select one of the
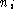 , form the
corresponding bond, and drop it from the list.
, form the
corresponding bond, and drop it from the list.
- 6.61. If the
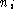 list is non-null,
execute steps 6.41 through 6.43.
list is non-null,
execute steps 6.41 through 6.43. - 6.62. Exit.
Steps 6.61 and 6.62 seem to be redundant (and consequently confusing). The situations they would cover are already covered by steps 6.41 through 6.43 anyway, so it would seem simpler just to stipulate an unconditional transfer to 6.41 immediately after 6.6.
- 6.61. If the
Note that the bonding algorithm, as presented, does not rule out the formation of ``crossed over'' bonds. For example, in the configuration of figure 4, the algorithm would result in the formation of a crossed over bond. This seems counter intuitive, and contrary to the chemical inspiration of the model. However, in the absence of some constraint to the contrary in the algorithm, we must assume that it is intended to be allowed. There is no explicit discussion of this, and it is not apparent that it would contribute anything of significance to the phenomenology of the model.
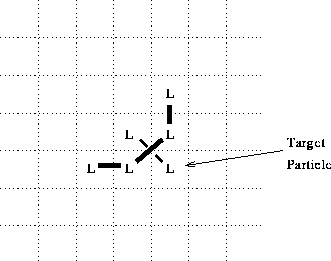
Figure 4: Scenario for formation of crossed bond.
This final top-level step of the algorithm is invoked as a subprocedure from the disintegration reaction (step 5.11). While it is not explicitly stated, we assume this subprocedure receives, as an argument, a position where an L particle has just disintegrated. The essential effect of this subprocedure is to ``reform'', as far as possible, bonds in the neighborhood of this position.
``Re-form'' is something of a misnomer here: the bonds that have actually been broken as a result of the disintegration obviously cannot be ``reformed'', since the relevant L particle is no longer present. But the step is not even restricted just to ``reforming'' bonds with L particles that were previously bonded to the disintegrated L; in fact, this step blindly attempts to form bonds among all L particles in the neighborhood of the disintegration site, regardless of whether they were involved in, or otherwise affected by, the disintegration. Furthermore, it is perfectly possible that some of the L particles that are processed for bonding here may yet actually be subject to disintegration on this same timestep.
The rebonding algorithm itself is deceptively short; it actually hides some moderately complex processing. As with step 6, bonding is effected preferentially on L particles that are already singly bonded; bonding to or between free L particles is then considered secondarily.
- 7.1. Form a list of all neighbor
positions
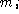 occupied by singly bonded L's.
occupied by singly bonded L's. - 7.2. Form a second list,
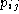 , of
pairs of the
, of
pairs of the 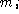 which can be bonded.
which can be bonded.
The force of the phrase ``can be bonded'' is not made explicit here, so we must ask why particular pairs may be excluded. Three distinct cases arise.
Firstly, it is clear that only pairs of L particles that are adjacent to each other are eligible for bonding to each other.
Secondly--and trivially--some of the pairs of adjacent, singly bonded, L particles may already be bonded to each other.
Finally, since each of the L particles currently under consideration is already singly bonded, the proposed new bond would, in each case, be a second bond--and would therefore cause a new bond angle to be established at each of the two particles involved. If either of these two new bond angles would be less than
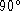 then, presumably, that pair must be excluded
from consideration.
then, presumably, that pair must be excluded
from consideration. - 7.3. If there are any
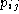 , choose a
maximal subset and form the bonds. Remove the L's
involved from the list
, choose a
maximal subset and form the bonds. Remove the L's
involved from the list  .
.
The difficulty here is with the phrase ``maximal subset'', which is not explained in any detail.
However, the idea seems to be as follows. Of the pairs listed in p (say there are k entries in this list), it may not be possible to form all the corresponding bonds, because there could be conflicts between them. Specifically, if the same (singly bonded) L particle occurs in two different pairs then, clearly, only one of those two pairs can be chosen for bonding. So, the requirement of the algorithm seems to be that various possible subsets of pairs may have to be investigated. This would start by considering whether all (q) of the pairs can indeed be bonded (i.e. there are actually no conflicts). If so, they are all bonded, and control can pass to the next step; but, if not, then all possible subsets of k-1 of the pairs must be considered. If there are no conflicts in one of these subsets, then all of those bonds should be formed (and if there are multiple such, mutually compatible, subsets, then one should presumably be chosen uniformly at random). If no mutually compatible subset of k-1 pairs exists, then the subsets of k-2 pairs should be considered next and so on. Clearly this process will terminate at k=1 since there can be no conflicts in such subsets.
There is nothing fundamentally difficult about carrying out this procedure. However, it seems extraordinarily complex, for no obvious or explained benefit. A much simpler alternative--which would be expected to yield essentially the same phenomenology--would be to simply pick an element of p at random, and form that bond; then remove any other elements from p that are no longer eligible, and then pick another at random for bonding; continue this process until p is empty. Of course, this procedure is not deterministically guaranteed to generate a ``maximal'' subset of bonds; but it would seem very strange indeed if the phenomenology of the system depended critically on this.
Nonetheless, it seems that any strict implementation of the algorithm will be required to search deterministically for a maximal subset of p.
- 7.4. Add to the bond
 any neighbor
locations occupied by free L's.
any neighbor
locations occupied by free L's.
The list m was potentially reduced at step 7.3, by removing from it the positions of any singly bonded L particles that have now become doubly bonded. Step 7.4 now simply adds to this list the positions of any free L particles in the neighborhood of the disintegration site. Note carefully that the list m now potentially contains both free and singly bonded L particles. This should be clearly distinguished from the situation in top-level step 6, where two separate lists were maintained for free and singly bonded links.
- 7.5. Execute steps 7.1 through 7.3, then
exit.
The reference to step ``7.1'' here must be a typographical error: since step 7.1 is concerned with forming the list m in the first place; regenerating it at this point would be incoherent. So we must assume that the intention is to ``reexecute'' steps 7.2 and 7.3 only. Even this ``reexecution'' is not completely straightforward. In particular, steps 7.2 and 7.3 must now be interpreted as applying to the more general case that the list m contains a mix of both singly bonded and free L particles, whereas in the original context it could be assumed that it contained singly bonded particles only.
 5 External Review
5 External Review
 4 Internal Algorithm Review
4 Internal Algorithm Review
 4.1 Conventions
4.1 Conventions